Kraftmoment
$$M = F \cdot L$$
där
\(M=\) kraftmomentet (Nm)
\(F=\) vridande kraften (N)
\(L=\) momentarmen (m)
Jämviktslagen vid kraftmoment
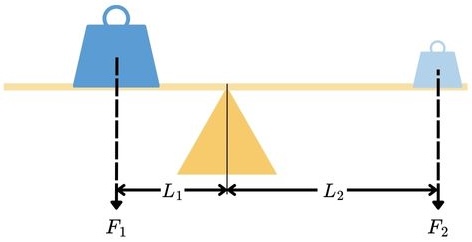
\[F_1 \cdot L_1 = F_2 \cdot L_2\]
Vid olika antal krafter på ömse sidor om vridningsaxeln
\[\sum F_k \cdot L_k = \sum F_n \cdot L_n\]

Kraftmomentet M är produkten av den vridande kraften F och momentarmen L.
\[\text{kraftmoment} = \text{vridande kraft} \cdot\text{momentarm}\] \[M = F \cdot L\] Momentarmen L är det vinkelräta avståndet mellan vridningsaxeln och kraften F:s riktningslinje.
Jämviktslagen vid kraftmoment
Vid jämvikt är kraftmomentet medurs lika stort som kraftmomentet moturs räknat från vridningsaxeln. Vid en kraft verkande på ömse sidor om vridningsaxeln blir
\[M_{\text{med}} = F_1 \cdot L_1\] \[M_{\text{mot}}=F_2 \cdot L_2\] och vid momentjämvikt
\[M_{\text{med}} = M_{\text{mot}} \Rightarrow F_1 \cdot L_1 = F_2 \cdot L_2\] eller vid olika antal krafter på ömse sidor om vridningsaxeln
\[\sum F_k \cdot L_k = \sum F_n \cdot L_n\]
Tre olika jämviktsvillkor måste vara uppfyllda för att ett föremål ska befinna sig i jämvikt och i vila
- \(\rightarrow\) Resultanten (summan) av horisontalkrafterna som påverkar föremålet måste vara 0
- \(\uparrow\) Resultanten (summan) av vertikalkrafterna som påverkar föremålet måste vara 0
- Summan av kraftmomenten åt ena hållet måste vara lika med summan av kraftmomenten åt det motsatta hållet
