Hastighet
Vid likformig hastighet, dvs då hastigheten är konstant över förflyttningstiden
$$v = \frac{s}{t} =\frac{\Delta s}{\Delta t}$$ vilket följaktligen också blir medelhastigheten, och \(s=v \cdot t\)
\(v= \text{hastighet i meter/sekunder (m/s)}\)
\(s= \text{förflyttningssträckan i m}\)
\(t= \text{förflyttningstiden i s}\)
Momentanhastighet
Momentanhastigheten är hastigheten i varje givet ögonblick, dvs när \(\Delta t \rightarrow 0\). Vi kan också skriva momentanhastigheten som $$v_{momentan}=\frac{\mathrm{d} s}{\mathrm{d}t}$$ vilket är identiskt med tangentens lutning i punkten på en sträcka-tid graf, alltså derivatan av sträckan med avseende på tiden i just den punkten.
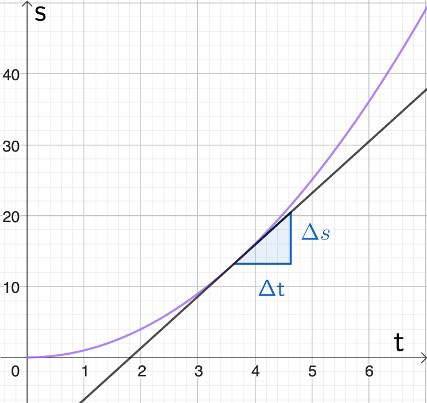
Medelhastighet
$$v_{\mathrm{m}}=\frac{\Delta s}{\Delta t}=\frac{s_1-s_0}{t_1-t_0}$$
\(v_{\mathrm{m}}=\text{medelhastighet}\)
\(\Delta s= \text{förflyttningssträckan}\)
\(\Delta t= \text{tidsintervall för att fullgöra sträckan}\; \Delta s\)
